Orthogonal Trajectories
We have seen before (see separable equations for example) that the solutions of a differential equation may be given by an implicit equation with a parameter something like
This is an equation describing a family of curves. Whenever we fix the parameter C we get one curve and vice-versa. For example, consider the families of curves
where m and C are parameters. Clearly, we may change the names of the variables and still have the same geometric curves. For example, the above families define the same geometric object as
Note that the first family describes all the lines passing by the origin (0,0) while the second the family describes all the circles centered at the origin (including the limit case when the radius 0 which reduces to the single point (0,0)) (see the pictures below).
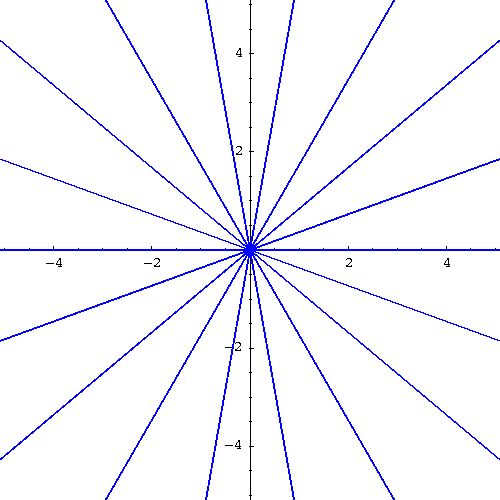
|
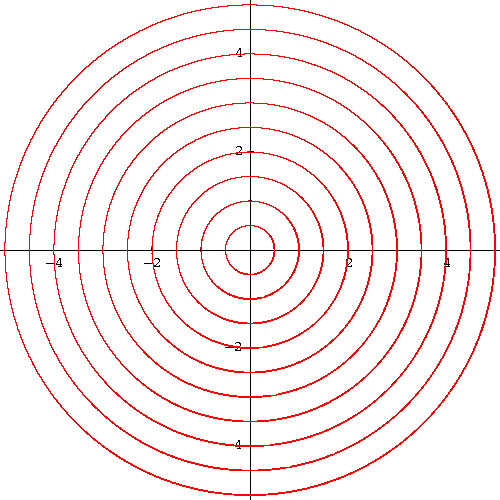
|
One may ask whether any family of curves may be generated from a differential equation? In general, the answer is no. Let us see how to proceed if the answer were to be yes. First differentiate with respect to x, and get a new equation involving in general x, y,
Example. Find the differential equation satisfied by the family
Answer. We differentiate with respect to x, to get
Since we have
then we get
You may want to do some algebra to make the new equation easy to read. The next step is to rewrite this equation in the explicit form
this is the desired differential equation.
Example. Find the differential equation (in the explicit form) satisfied by the family
Answer. We have already found the differential equation in the implicit form
Algebraic manipulations give
Let us reconsider the example of the two families
If we draw the two families together on the same graph we get
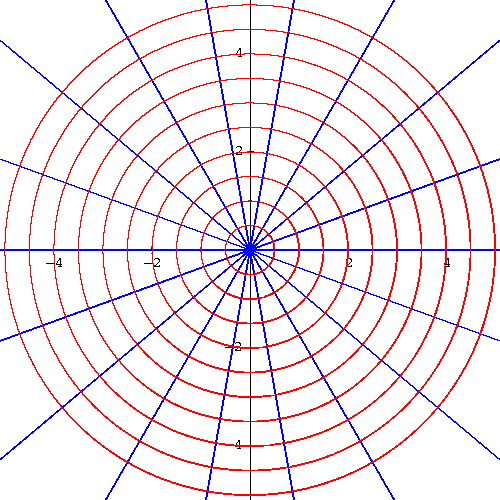
|
Definition. Consider two families of curves
For example, we have seen that the families y = m x and
Given a family of curves
The answer to this question has many implications in many areas such as physics, fluid-dynamics, etc... In general this question is very difficult. But in some cases, we may be able to carry on the calculations and find the orthogonal family. Let us show how.
Consider the family of curves
We know that for any curve from the family passing by the point (x,y), the slope of the tangent at this point is f(x,y). Hence the slope of the line perpendicular (or orthogonal) to this tangent is
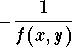 which happens to be the slope of the tangent line to the orthogonal curve passing by the point (x,y). In other words, the family of orthogonal curves are solutions to the differential equation
which happens to be the slope of the tangent line to the orthogonal curve passing by the point (x,y). In other words, the family of orthogonal curves are solutions to the differential equation
From this we see what we have to do. Indeed consider a family of curves
- Step 1. Find the associated differential equation.
- Step 2. Rewrite this differential equation in the explicit form

- Step 3. Write down the differential equation associated to the orthogonal family

- Step 4. Solve the new equation. The solutions are exactly the family of orthogonal curves.
- Step 5. You may be asked to give a geometric view of the two families. Also you may be asked to find a specific curve from the orthogonal family (something like an IVP).
Answer. First, we look for the differential equation satisfied by the circles. We differentiate with respect to the variable x to get
We rewrite this equation in the explicit form
Next we write down the equation for the orthogonal family
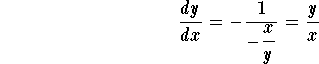
This is a linear as well as a separable equation. If we use the technique of linear equations, we get the integrating factor
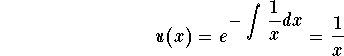
which gives
We recognize the family of lines and we confirm our earlier observation (that the two families are indeed orthogonal).
This example is somehow easy and was given here to illustrate the technique.
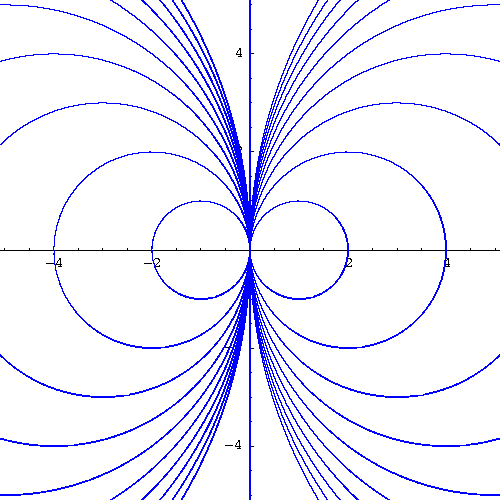
Example. Find the orthogonal family to the family of circles
|
Hence the differential equation for the orthogonal family is
We recognize an homogeneous equation. Let us use the technique developed to solve this kind of equations. Consider the new variable
and
Hence we have
Algebraic manipulations imply
This is a separable equation. The constant solutions are given by
which gives z=0. The non-constant solutions are found once we separate the variables
and then we integrate
Before we perform the integration for the left-hand side, we need to use partial decomposition technique. We have
We will leave the details to you to show that A = 1, B=-2, and C=0. Hence we have
Hence
which is equivalent to
where
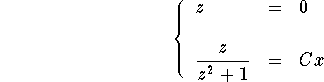
Going back to the variable y, we get
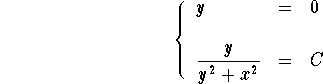
which is equivalent to

We recognize a family of circles centered on the y-axis and the line y=0 (the x-axis which was easy to guess, isn't it?)
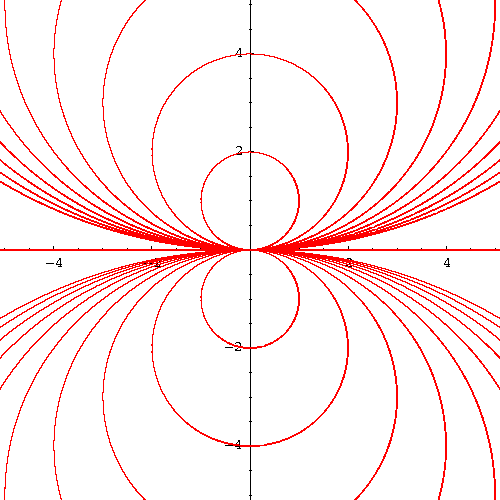
|
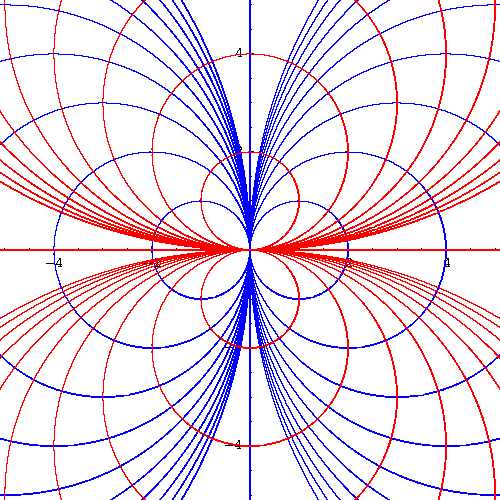
|

 S.O.S MATHematics home page
S.O.S MATHematics home page 

Tidak ada komentar:
Posting Komentar