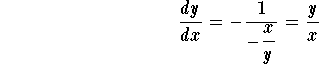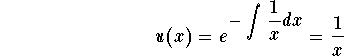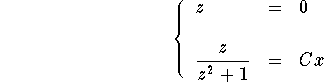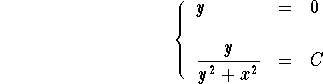Bessel functions
Cylinder functions of the first kind. A Bessel function of order

can be defined as the series
 | (*) |
which converges throughout the plane. A Bessel function of order

is the solution of the corresponding
Bessel equation. If the argument and the order

are real numbers, the Bessel function is real, and its graph has the
form of a damped vibration (Fig.); if the order is even, the Bessel
function is even, if odd, it is odd.

Figure: b015840a
Graphs of the functions

and

.
The behaviour of a Bessel function in a neighbourhood of zero is given by the first term of the series (*); for large

, the asymptotic representation
holds. The zeros of a Bessel function (i.e. the roots of the equation

) are simple, and the zeros of

are situated between the zeros of

. Bessel functions of "half-integral" order

are expressible by trigonometric functions; in particular
The Bessel functions

(where

are the positive zeros of

,

) form an orthogonal system with weight

in the interval

. Under certain conditions the following expansion is valid:
In an infinite interval this expansion is replaced by the Fourier–Bessel integral
The following formulas play an important role in the theory of Bessel functions and their applications:
1) the integral representation
2) the generating function
3) the addition theorem for Bessel functions of order zero
4) the recurrence formulas
For references, see
Cylinder functions.
 can be defined as the series
can be defined as the series

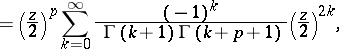
 is the solution of the corresponding Bessel equation. If the argument and the order
is the solution of the corresponding Bessel equation. If the argument and the order  are real numbers, the Bessel function is real, and its graph has the
form of a damped vibration (Fig.); if the order is even, the Bessel
function is even, if odd, it is odd.
are real numbers, the Bessel function is real, and its graph has the
form of a damped vibration (Fig.); if the order is even, the Bessel
function is even, if odd, it is odd.

 and
and  .
.
 , the asymptotic representation
, the asymptotic representation
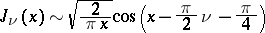
 ) are simple, and the zeros of
) are simple, and the zeros of  are situated between the zeros of
are situated between the zeros of  . Bessel functions of "half-integral" order
. Bessel functions of "half-integral" order  are expressible by trigonometric functions; in particular
are expressible by trigonometric functions; in particular
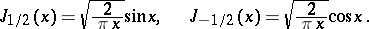
 (where
(where  are the positive zeros of
are the positive zeros of  ,
,  ) form an orthogonal system with weight
) form an orthogonal system with weight  in the interval
in the interval  . Under certain conditions the following expansion is valid:
. Under certain conditions the following expansion is valid:
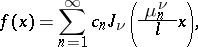
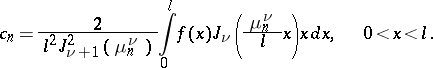
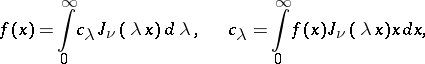
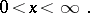
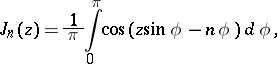
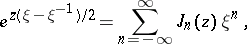
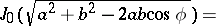

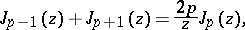
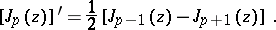

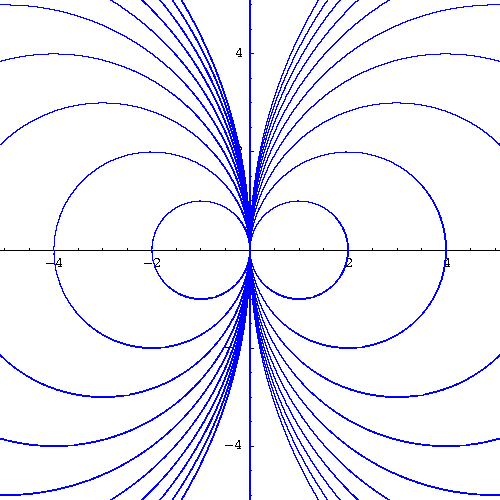
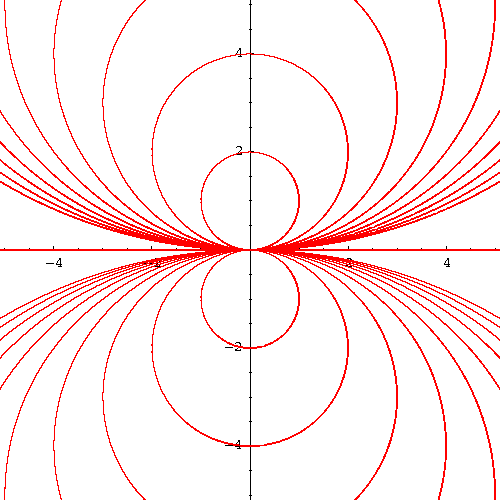
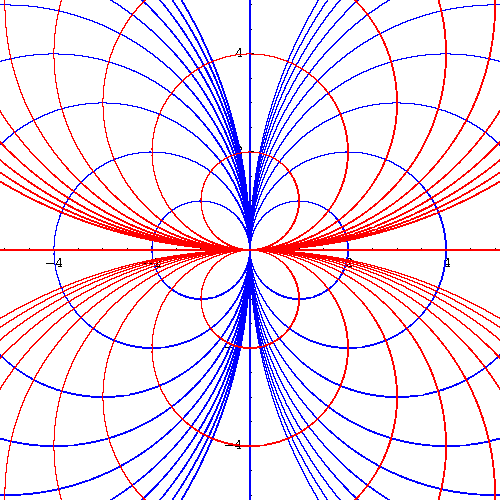
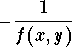 which happens to be the slope of the tangent line to the orthogonal curve passing by the point (x,y). In other words, the family of orthogonal curves are solutions to the differential equation
which happens to be the slope of the tangent line to the orthogonal curve passing by the point (x,y). In other words, the family of orthogonal curves are solutions to the differential equation